The monitoring feature uses the row identifiers in the prediction data and ground truth data to match the predicted and expected value. Based on those matches, it calculates the model quality metrics.
By default, model quality checks are scheduled to occur daily at 12 PM UTC.
|
Note
|
Prediction data is analyzed through 23:59 of the previous day. Data from the current day is not included. Domino reads the timestamps in the dataset if they are present; if not, it uses the ingestion timestamp. |
Classification models and regression models show different prediction quality metrics. See Metrics for classification and regression models for details.
If you are looking at a classification model, a confusion matrix and classification report for the data in the selected time range is shown in a Charts section under the metrics table. See classification models for details.
For classification models:
-
Model monitoring uses weighted method to calculate the metrics.
-
AUC, ROC, Log Loss, and Gini Norm are only calculated if the Predication Probability type is declared as part of the schema. See the Note in Monitoring Config JSON.
-
Sample Weights is used in calculations for the Gini Norm metric only.
Modify the test features
-
If you are using the monitoring feature for a Domino endpoint:
-
Go to Configure monitoring > Data.
-
In the Configure Data dialog, in the Ground Truth Data section, click open this model.
-
-
If you are using the Model Monitor, in the navigation pane, click Model Monitor. Select the model that you want to monitor and then click Model Quality.
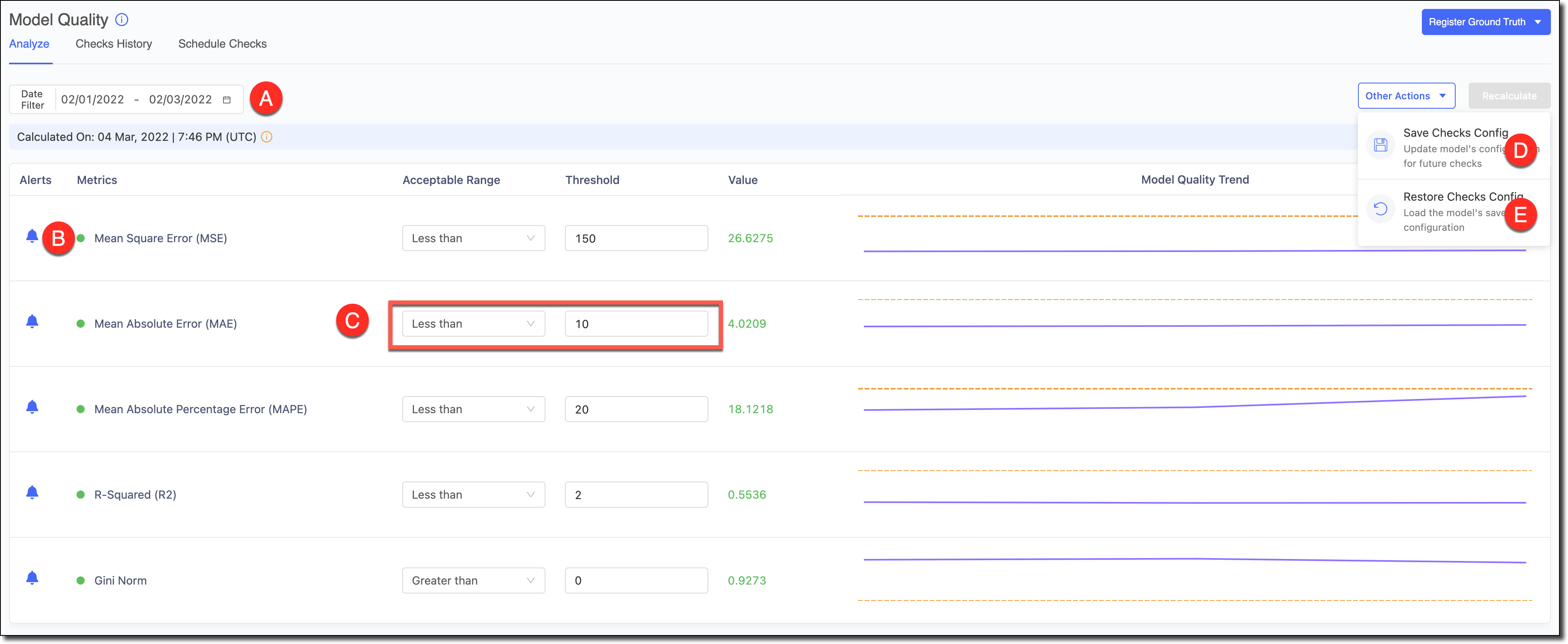
A - Use the Date Filter to refine the date range and review the Model Quality and its trends for specific time periods.
B - To reduce alert noise, click the bell icon next to a feature to disable alerts and exclude it from the Scheduled Checks.
C - Select the Acceptable Range and the Threshold. Click Recalculate to see the results.
D - If you made changes to the tests and want to set them as the defaults for the model in subsequent automated checks, go to Other Actions > Save Checks Config to save the changes.
E - If you experimented with changes to the tests and wanted to load the model’s default configuration to reset the table, go to *Other
Classification models
The following are the supported prediction quality metrics for Classification models. All metrics are calculated using the weighted average method with the weight relating to the proportion of occurrences of a prediction class in the dataset.
- Accuracy
-
Accuracy is the most common metric used to evaluate the performance of a classification model. It is calculated as the proportion of examples in the evaluation dataset that were predicted correctly, divided by all predictions that were made on the evaluation dataset. + A confusion matrix represents the model’s true positives, true negatives, false positives, and false negatives for each prediction class. The classification accuracy can be calculated from this confusion matrix as the sum of true positives and true negatives divided by the sum of the true positives, true negatives, false positives and false negatives.
- Precision
-
Precision quantifies the number of positive identifications that were actually correct. It is defined as the ratio of true positives to the sum of true positives and false positives
- Recall
-
Recall quantifies the proportion of positive identifications was actually correct. It is defined as the ratio of true positives to the sum of true positives and false negatives
- F1
-
The F(n) score allows us to give precision or recall a higher weight based on what is important to the use case being evaluated. For F1, both precision and recall are given equal weight and is calculated as the harmonic mean of the precision and recall. + The formula for F1 is (2 * precision * recall) / (precision + recall)
- ROC
-
An ROC curve (receiver operating characteristic curve) is a graph showing the performance of a classification model at all classification thresholds. This curve plots two parameters: true positive rate on the y-axis and false positive rate on the x-axis. Typically, lowering the classification threshold results in increasing both false positives and true positives and the curve is used to decide a classification threshold that is a good tradeoff between the two.
- AUC
-
AUC stands for Area under the ROC curve and measures the 2D area under the ROC curve. The AUC provides an aggregate measure of performance across all possible classification thresholds. AUC ranges in value from 0 to 1. A model whose predictions are 100% wrong has an AUC of 0 and one whose predictions are 100% correct has an AUC of 1. The AUC is desirable as it measures the quality of the model’s predictions irrespective of what classification threshold is chosen.
- Log Loss
-
Log-loss is indicative of how close the prediction probability is to the corresponding actual/true value (0 or 1 in case of binary classification). The more the predicted probability diverges from the actual value, the higher is the log-loss value. It’s hard to interpret raw log-loss values, but log-loss is a good metric for comparing models. For any given model, a lower log-loss value means better predictions
- Gini coefficient (Normalized)
-
The (normalized) Gini coefficient gets its inspiration from the Lorentz curve in economics and is typically used when the datasets are imbalanced. In the context of Machine Learning the equivalent of the Lorenz curve is built using the values of the (predicted) class probabilities as opposed to “income” that is used in economics models. The Gini coefficient is then defined as the area under the Lorentz curve. Dividing the Gini coefficient computed from the Lorenz curve of the predicted class probabilities by the Gini coefficient computed from the actual class probabilities results in a normalized Gini coefficient for classification models.
Regression models
The following are the supported prediction quality metrics for Regression models.
- Mean Square Error (MSE)
-
Mean squared error (MSE) measures the amount of error (also called residual) in regression models. It assesses the average squared difference between the observed and predicted values. When a model has no error, the MSE equals zero. As model error increases, its value increases. The mean squared error is also known as the mean squared deviation (MSD) and is calculated by dividing the sum of squared errors by the sample size.
- Mean Absolute Error (MAE)
-
The MAE is computed by taking the average of the absolute difference between the actual or true values and the values that are predicted by the regression model for every datapoint in the evaluation dataset. It is therefore measuring the average magnitude of errors of the predictions irrespective of whether the prediction was less than or greater than the actual value.
- Mean Absolute Percentage (MAPE)
-
Mean absolute percentage error (MAPE) is commonly used as a loss function for regression problems and in model evaluation. It is the percentage equivalent of MAE and as it is a percentage is an intuitive way to quantify on average how far the model’s predictions are off from the actual values. Both MAPE and MAE are robust to outliers but have the disadvantage of being biased towards predictions that are less than the actual values themselves.
- R-Squared (R2)
-
R-Squared (R2) is a statistical measure of how close the data is to the fitted regression hyperplane.It is defined as the percentage of variation in the target variable that is explained by the regression model. R-Squared (R2) lies between 0 and 1 ( or 0% and 100%) and 0 (0%) indicates that the model explains none of the variability of the target data around its mean and 1 (100%) indicates that the model explains all the variability of the target data around its mean
- Gini (Normalized)
-
The (normalized) Gini coefficient gets its inspiration from the Lorentz curve in economics and is typically used when the datasets are imbalanced i.e there are big (and) small values in the dataset. In the context of regression models, the equivalent of the Lorenz curve is built using the predicted values of the target variable as opposed to “income” that is used in the case of economics models. The Gini coefficient is then defined as the area under the Lorenz curve. Dividing the Gini coefficient computed from the Lorenz curve of the predictions by the Gini coefficient computed from the actual values results in a normalized Gini coefficient for regression models.
